Continuous Random Variable

Class Name

• RContinuousRandomVariable

Location in Objects Pane

• Models > Parameter > Random Variable > Continuous

Properties

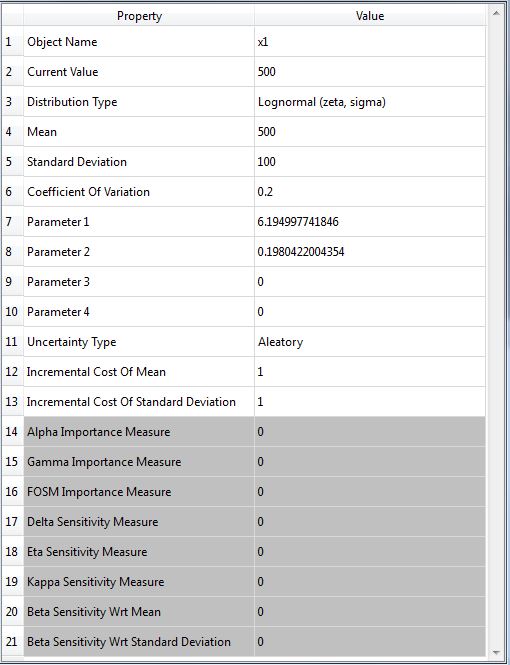
Object Name

• Name of the object in Rt
• Allowable characters are upper-case and lower-case letters, numbers, and underscore (“_”).
• The name is unique and case-sensitive.

Current Value

• Current realization of the random variable

Distribution Type

• Probability distribution of the random variable
• The distribution type is followed by the distribution parameters inside parentheses.
• These parameters, respectively, correspond to Parameter 1 to Parameter 4 that appear as some other properties below.
• If, for instance, only two parameters appear inside parentheses for a particular distribution type, only Parameter 1 and Parameter 2 are applicable to that distribution.
• If the “User-defined” distribution is selected, two more properties are shown, namely, X Points and PDF Points, described below.

Mean

• Mean of the random variable
• It can be a number or another parameter.
• If changed, the values of Coefficient Of Variation and Parameter 1 to Parameter 4 properties are re-calculated.

Standard Deviation

• Standard deviation of the random variable
• It can be a number or another parameter.
• If changed, the values of Coefficient Of Variation and Parameter 1 to Parameter 4 properties are re-calculated.

Coefficient Of Variation

• Coefficient of variation of the random variable
• It is a standardized measure of dispersion of a probability distribution.
• If changed, the values of Standard Deviation and Parameter 1 to Parameter 4 properties are re-calculated.

Parameter 1

• The first parameter of the random variable, as appears inside the parentheses in the Distribution Type.
• If changed, the values of Mean, Standard Deviation, and Coefficient Of Variation properties are re-calculated.

Parameter 2

• The second parameter of the random variable, as appears inside the parentheses in the Distribution Type, if applicable.
• If changed, the values of Mean, Standard Deviation, and Coefficient Of Variation properties are re-calculated.

Parameter 3

• The third parameter of the random variable, as appears inside the parentheses in the Distribution Type, if applicable.
• If changed, the values of Mean, Standard Deviation, and Coefficient Of Variation properties are re-calculated.

Parameter 4

• The fourth parameter of the random variable, as appears inside the parentheses in the Distribution Type, if applicable.
• If changed, the values of Mean, Standard Deviation, and Coefficient Of Variation properties are re-calculated.

Uncertainty Type

• Indicates whether the random variable describes an “Aleatory” or an “Epistemic” uncertainty.
• This is employed, for instance, when computing model response standard deviation sensitivities in FORM.
• For more information, see Der Kiureghian (2009)

X Points

• Vector of random variable realizations for which the PDF values are given to the property below, i.e., PDF Points in a “User Defined” distribution.

PDF Points

• Vector of PDF values of the random variable realizations that are given to the property above, i.e., X Points in a “User Defined” distribution.

Read-only Properties

Alpha Importance Measure

• Element of the \(\boldsymbol{\alpha}\) importance vector, computed in FORM, that corresponds to this random variable.
• \(\boldsymbol{\alpha}\) is a unit vector that indicates the relative importance of the random variables involved in a FORM analysis when correlations are neglected/non-existent.
• For more information, see Der Kiureghian (2005).

Gamma Importance Measure

• Element of the \(\boldsymbol{\gamma}\) importance vector, computed in FORM, that corresponds to this random variable.
• \(\boldsymbol{\gamma}\) is a unit vector that indicates the relative importance of the random variables involved in a FORM analysis when correlations are considered.
• For more information, see Der Kiureghian (2005).

FOSM Importance Measure

• Element of the FOSM importance vector, \(\boldsymbol{\omega}\), computed in FOSM, that corresponds to this random variable.
• \(\boldsymbol{\omega}\) is a unit vector that indicates the relative importance of the random variables involved in a FOSM analysis.
• For more information, see Der Kiureghian (2005).
• \(\boldsymbol{\omega}\) is computed as
$$\boldsymbol{\omega}\ = - {\nabla {g^T}{\mathbf{D _ X}} \over {\left\| {\nabla {g^T}{\mathbf{D_X}}} \right\|}}$$ where \(\nabla {g}\) = gradient of the limit-state function, \(g\), and \(\mathbf{D_X}\) = standard deviation matrix of random variables, \(\mathbf{X}\).

Delta Sensitivity Measure

• Element of the \(\boldsymbol{\delta}\) sensitivity vector, that corresponds to this random variable.
• \(\boldsymbol{\delta}\) is a dimensionless vector that is computed by multiplying the standard deviation matrix by the gradient of the reliability index with respect to the mean of random variables.
• For more information, see Der Kiureghian (2005).

Eta Sensitivity Measure

• Element of the \(\boldsymbol{\eta}\) sensitivity vector, that corresponds to this random variable
• \(\boldsymbol{\eta}\) is a dimensionless vector that is computed by multiplying the standard deviation matrix by the gradient of the reliability index with respect to the standard deviation of random variables
• For more information, see Der Kiureghian (2005)

Kappa Sensitivity Measure

• Element of the \(\boldsymbol{\kappa}\) sensitivity vector, that corresponds to this random variable.
• \(\boldsymbol{\kappa}\) is a dimensionless vector equal to the gradient of the reliability index with respect to the coefficient of variation of random variables.

Beta Sensitivity Wrt Mean

• Derivative of the reliability index, \({\beta}\), with respect to the mean of this random variable

Beta Sensitivity Wrt Standard Deviation

• Derivative of the reliability index, \({\beta}\), with respect to the standard deviation of this random variable

Right-click Menu

Remove

• Removes the object.

Plot PDF

• Plots the probability density function of the random variable in the range of mean ± three standard deviations.

Plot CDF

• Plots the cumulative distribution function of the random variable in the range of mean ± three standard deviations.

Plot Inverse CDF

• Plots the inverse cumulative distribution function of the random variable in the range of mean ± three standard deviations

Get PDF

• Prints the probability density function value for a given random variable realization on the output pane.

Get CDF

• Prints the cumulative distribution function value for a given random variable realization on the output pane.

Get Inverse CDF

• Prints the inverse cumulative distribution function value, i.e., the realization, for a given probability on the output pane.

Types of Distribution

• Beta Distribution
• Chi-Squared Distribution
• Exponential Distribution
• Gamma Distribution
• Gumbel Distribution
• Laplace Distribution
• Logisitic Distribution
• Lognormal Distribution
• Normal Distribution
• Rayleigh Distribution
• t Distribution
• Uniform Distribution
• Weibull Distribution
• Wald Distribution
• Levy Distribution
• Irwin-Hall Distribution
• Birnbaum-Saunders Distribution
• Type-2 Gumbel Distribution
• Pareto Distribution
• F Distribution
• Arcsine Distribution

Beta Distribution

Chi-Squared Distribution

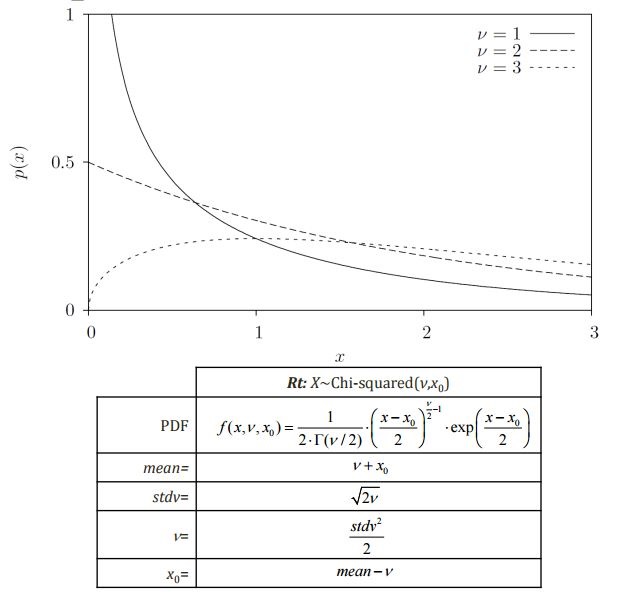
Exponential Distribution

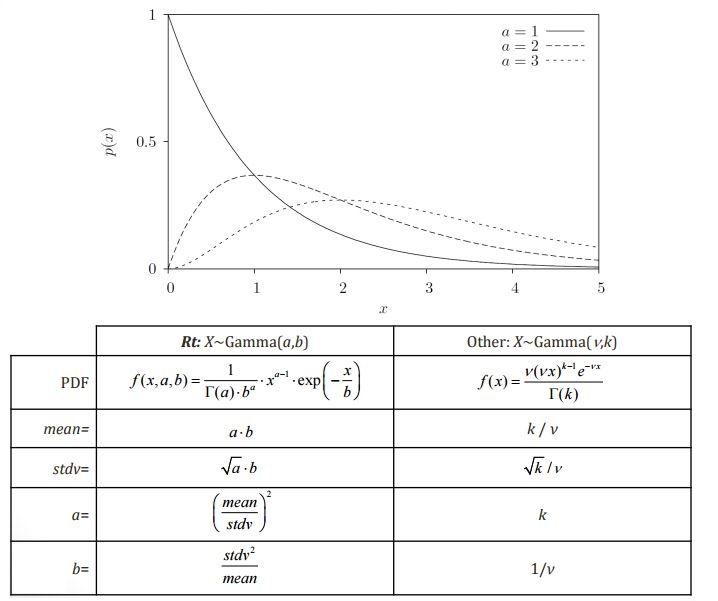
Gamma Distribution

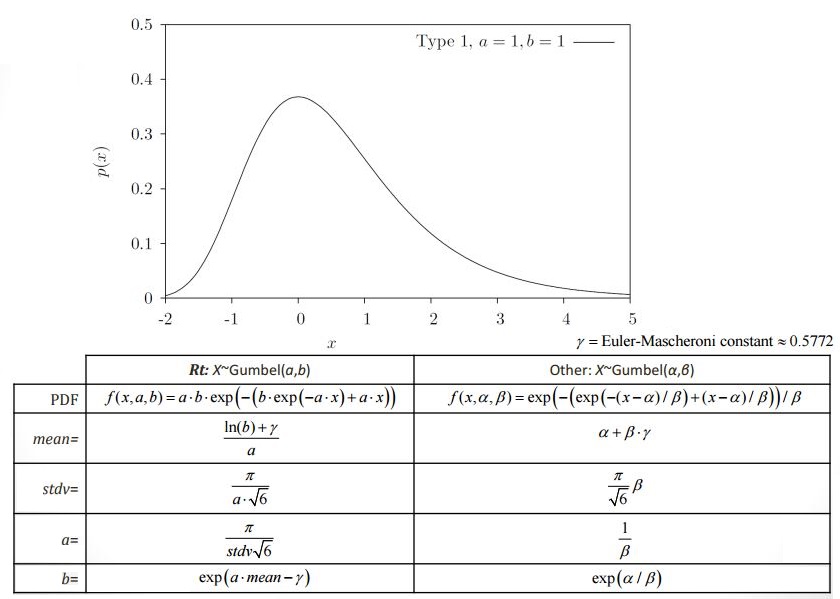
Gumbel Distribution

Laplace Distribution

Logistic Distribution

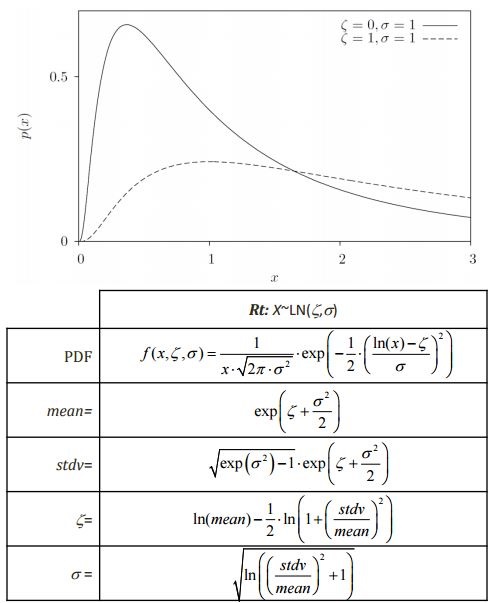
Lognormal Distribution

Normal Distribution

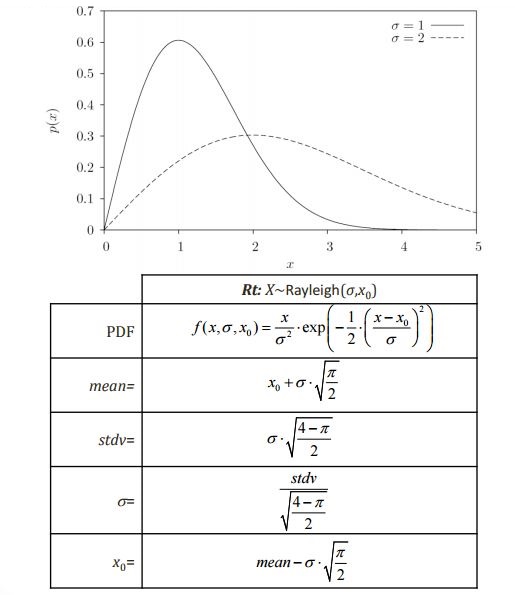
Rayleigh Distribution

t Distribution

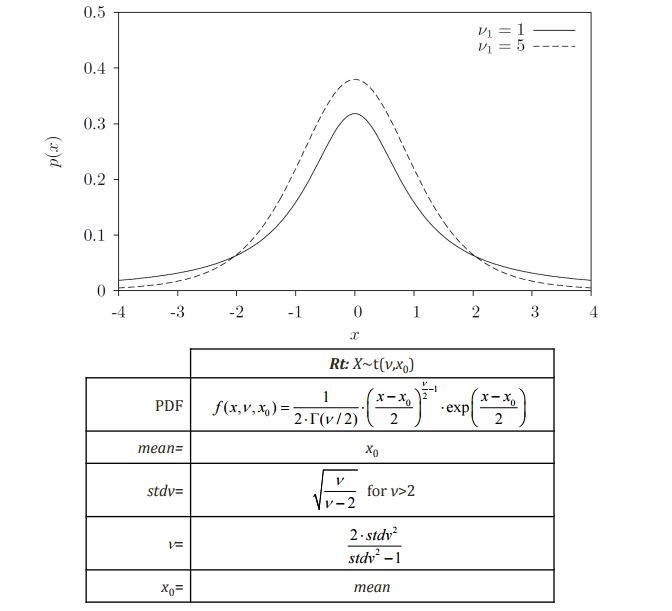
Uniform Distribution

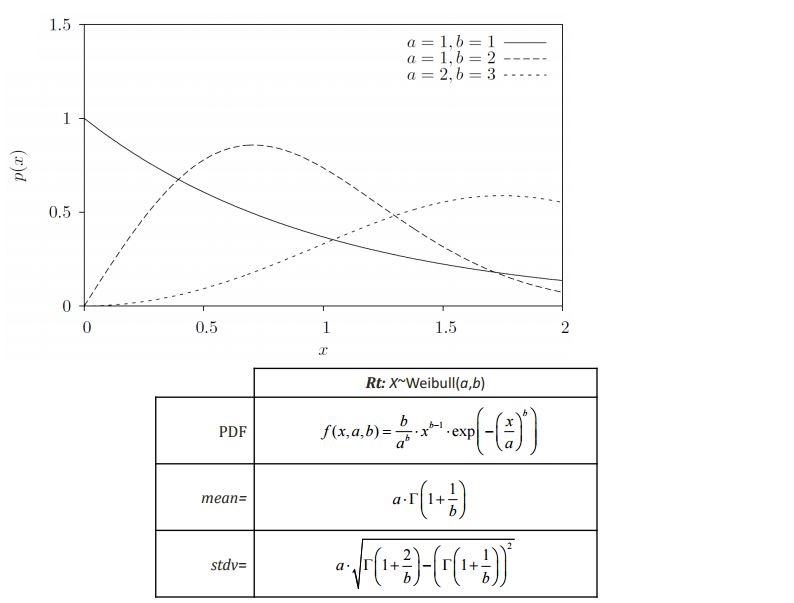
Weibull Distribution

Wald Distribution

Levy Distribution

Irvin-Hall Distribution

Birnbaum-Saunders Distribution

Type-2 Gumbel Distribution

Pareto Distribution

F Distribution

Arcsine Distribution

References

• Der Kiureghian, A. (2005). First-and second-order reliability methods. In E. Nikolaidis, D. M. Ghiocel, & S. Singhal (Eds.), Engineering design reliability handbook. Boca Raton, Florida: CRC Press
• Der Kiureghian, A., & Ditlevsen, O. (2009). Aleatory or epistemic? Does it matter? Structural Safety, 31(2), 105–112